Gibbs
17.1 When to Use Gibbs
Given a directed acyclic graph, covariance or raw data, and a prior distribution over the model’s parameters , the Gibbs sampler draws a sample from the posterior distribution over the parameters given the data. This sample can in turn be used in a variety of ways to provide estimates of the parameters of a model. For example, as a point estimate for a parameter qj one can use the median of qj in the Gibbs sample from the posterior, which we denote as: qMedian. For a 95% confidence region around for, one can use the interval from the 2.5th percentile to the 97.5th percentile in the Gibbs sample: q.025 - q.975. The Gibbs command automates the generation of the sample, but does not currently automatically calculate parameter estimates or confidence regions from the sample. In this chapter we will assume that the reader is already familiar with the basic concepts of parameter estimation: see Bollen (1989) for a good introduction. For a detailed description of the Gibbs sampler implemented in TETRAD III, see (Scheines, Hoijtink, and Boomsma, 1995).
A number of statistical packages such as LISREL, CALIS, and EQS. provide facilities for finding maximum likelihood (ML) estimates for the parameters of a linear structural equation model with normally distributed variables. The sampling distribution of the ML estimator is consistent, but only asymptotically normal (Bollen, 1989). In LISREL, EQS, and CALIS, etc., ML standard errors are calculated on the assumption that the sampling distribution of the ML estimator is normal, which is not true when the sample size is small (Boomsma, 1983). A Bayesian estimator calculates the posterior distribution over the parameters, given a prior and data. If the prior is “flat,” or “uninformative,” i.e., uniform, then the posterior is proportional to the likelihood. In this case the mode of the posterior is just the maximum likelihood. The Gibbs sample is drawn from the true posterior no matter what the sample size, and hence “standard errors” calculated from the Gibbs sample in a flat prior context give better estimates than those provided by LISREL, CALIS, and EQS.
The Gibbs sampler also allows the user to incorporate prior information about the parameter values in the form of a prior distribution. This in turn allows one to sensibly estimate “underidentified” models. Again, for more detail and examples, see (Scheines, et. al, 1995).
17.2 Using the Gibbs Module
Given a model, covariance or raw data, and prior distribution over the model’s parameters (possible vague), the Gibbs sampler provides a sample from the posterior distribution over the parameters. To run it, you must provide the following TETRAD input sections in text file:
1) /covariances or /continuousraw
2) /graph (coefficients are starting values)
3) /linearmodel (error variances are starting values)
Other information and options (including changes to the prior distribution over the parameters) are given interactively (see below). The output includes a comment in which the prior distribution is specified, and then the sample from the posterior. The latter is given in n rows, each of which contains the iteration number and then a value for each free parameter being estimated.
For concreteness, suppose that we are trying to estimate the effect of lead exposure (LE) on a the iq of a population of children in the U.S. As LE is notorious difficult to measure accurately with our indicator le, we might specify simple errors-in-variables model in Figure 17.1.
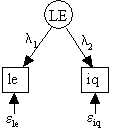
Fig. 17.1
There are five parameters in this model, whose population values we chose for simplicity and list in table 17.1:
|
Parameter |
Population Value |
|
Var(ele) |
1.0 |
|
Var(eIQ) |
1.0 |
|
Var(LE) |
1.0 |
|
l1 |
1.0 |
|
l2 |
-0.2 |
Table 17.1
Thus the population covariances S(q) for the measured variables le and iq is:
|
le |
iq |
|
2.0000 |
|
|
-0.2000 |
1.0400 |
Table 17.2
We drew a sample of size 100 from this population, which we show as the TETRAD input file gibbs100.dat below.
################
100.dat ##############:
/Covariance
100
le iq
1.9470
-0.2620 0.8619
################ gibbs100.dat ##############
Fig. 17.2
17.2.1 Running Gibbs
with a Flat Prior
To run the Gibbs sampler, you need input files that contain data, a model, and starting values for the parameters. The file gibbs100.dat (Fig. 17.2) contains the data, and the file gibbs100.mod contains the model and starting values (Fig. 17.3).
################ gibbs100.mod ##############:
/graph
LE le 1.0
LE iq -0.5
/linearmodel
Variable Dist. Type Parameters
le Normal
0.0000 1.0000
iq Normal 0.0000 1.0000
LE Normal
0.0000 1.0000
################ gibbs100.mod ##############
Fig. 17.3
By default, the variance of each latent variable is a fixed parameter, and the other parameters are free. However, the user can change these defaults interactively, as shown in Session 17-1. In the following example, we treat l1 as a fixed parameter, and Var(LE), Var(ele), Var(eIQ) and l2 as free parameters.
In order to calculate a posterior distribution over the parameters, a user must specify a prior distribution over the parameters. It is important to note that the prior distribution is not a distribution over the variables iq, le, and LE, but over the parameters of the model, Var(ele), Var(eIQ), Var(LE), l1, and l2. A user may in some cases feel that background knowledge does not provide any useful information about the values of the parameters. In this case the Gibbs command offers the user a chance to simply choose a "flat" prior over the free parameters, as shown in Session 17-1.
Even when a flat prior is chosen, however, the user must still specify starting values for each of the parameters. If the starting values are close to the population parameter values, the procedure may converge to the correct posterior distribution more quickly than if the starting values are far from the population parameter values. In this example, the starting values for each of the parameters is specified in start.val. In this example, from background knowledge the user knows that the effect of LE on le is positive, and so chooses 1.0 for the starting value. This is specified by the number following the line labelled "LE le" in the "/graph" section. The user also judges that the effect of LE on iq is likely to be negative and small, and so chooses a value of -0.2 for the most probable value of that edge coefficient. This is specified by the number following the line labelled "LE iq" in the "/graph" section. If the user has no opinion about whether the edge coefficient is positive or negative, he or she is free to choose an initial starting value of 0.0.
In start.val, the user must also specify the starting values for the variance of each error term based on background knowledge. Since the observed variance of le is 2.0, and Var(le) = Var(ele) + Var(LE), we can specify that half of le‘s variance is due to measurement error by assuming that Var(ele) = 1.0. We will assume that our best prior guess about the amount of measurement error is one half, so that the initial value of Var(ele) = 1.0. This number should be entered into the fourth column of the "le" row in a "linearmodel" section. In this example, the user has also entered 1.000 for the starting values for the error terms corresponding to iq and LE respectively. This is indicated by the 1.0000 in the fourth column in the lines corresponding to the variables iq and LE. The user should not choose an initial value of 0.000 for the variance of an error term, since this in effect makes the error term constant.
A lot of questions must be answered interactively to run the sampler, but almost all of them can just be answered with the default provided. We show a simple run with 15 interations in the screen session 17-1, into which we have written comments (italic and indented) of explanation.
Session 17-1
*************************************
We invoke the program
examples>tetrad3
TETRAD III - Unix Version 2.4
October, 1996
COPYRIGHT (C) 1996 by
Peter Spirtes, Richard Scheines,
Christopher Meek, and Clark Glymour
For help, type
"help"
Initializing Data
Structures
Input the covariance data
>in
Input File: gibbs100.dat
Erasing previous Evidence
Converting covariance
matrix to correlation matrix.
Input the model and starting values for the parameters.
>in
Input File: [gibbs100.dat]gibbs100.mod
Call the Gibbs sampler and specify the output file.
Erasing previous Evidence
>gibbs
Output file: gibbs100.outflat
Gibbs Parameter Estimation
Select a flat prior by hitting a carriage return <CR> to select the default given in brackets [f].
Flat or informative prior
(f\i)? [f] <CR>
Ask for 15 iterations, that is for a sample of size 15 from the posterior over the parameters.
Number of iterations: [100]: 15
The stretch is a parameter that controls the approximating distribution. See (Scheines, et. al., 1995). For now, choose the default.
stretch: [2]: <CR>
The rejection file contains information about draws in which the approximating distribution’s density was lower than the real density. Too many of these with values way above is not good. Again, see (Scheines, et. al., 1995).
Rejection Filename:
[gibbs.rej] <CR>
Now we must specify which parameters are fixed at their starting values, and which are free to be estimated. The default is to fix the variances of all latent variances. By typing “3 4” at the prompt for “List to change,” we fix the factor loading from LE to le at its starting value, and free the latent variance leaving four free parameters.
1: eV(le) Free
2: eV(iq) Free
3: eV(LE) Fixed
4: LE->le Free
5: LE->iq Free
List the numbers of any
parameters whose fixed/free
List the numbers of any
parameters whose fixed/free
status you wish to change
from its default value.
Separate them by at least
one space, and use no delimiters.
List to change = 3 4
The amended list is printed out so we can confirm that it is right or change it again if it isn’t.
1: eV(le) Free
2: eV(iq) Free
3: eV(LE) Free
4: LE->le Fixed
5: LE->iq Free
List OK? (y/n) [y] <CR>
Now the program prints out the inequality constraints on the parameters, which by default are only that variance paramaters be strictly positive.
1: eV(le) >
0.0000
2: eV(iq) >
0.0000
3: eV(LE) >
0.0000
4: LE->le none
5: LE->iq none
List the numbers of any
parameters upon which
you wish to impose
inequality constraints.
Separate them by at least
one space, and use no delimiters.
List to change = <CR>
By just hitting CR, we select the defaults, but the program makes sure by printing out the list again and asking us to confirm our choice.
1: eV(le) > 0.0000
2: eV(iq) > 0.0000
3: eV(LE) > 0.0000
4: LE->le none
5: LE->iq none
List OK? (y/n) [y] <CR>
Print all free parameters in output file (y\n)? [y] <CR>
Now the sampler has all the information it needs, and proceeds to print to the screen each time it has completed 10 interations, so you can monitor its progress on long runs.
Iter # 10
Finally, we exit TETRAD to Unix.
>exit
examples>
*************************************
The output file produced (gibbs100.outflat) is as follows.
################ gibbs100.outflat ##############
{Output file:
gibbs100.outflat
Graph file: gibbs100.mod
Data file: gibbs100.dat
Graph:
LE -> le LE ->
iq
Stretch: 2.0000
15 iterations
Prior distribution over
Model Parameters
is uninformative.
--------------------------
Starting Values for Parameters
Parameter Value Free/Fixed
-----------------------------------------
eV(le)
1.0000 Free
eV(iq)
1.0000 Free
eV(LE)
1.0000 Free
LE->le
1.0000 Fixed
LE->iq
-0.5000 Free
Equality and Inequality
constraints
(All error variances > 0)
-----------------------------------
None
Iter eV(le) eV(iq) eV(LE)
LE->iq }
1 1.2032 0.7631 1.1771 -0.1818
2 0.7771 0.8409 1.3960 -0.3070
3 0.6680 0.8004 1.2574 -0.1841
4 0.4471 0.8301 1.4946 -0.1631
5 0.5951 0.8668 1.1441 -0.4394
6 0.4941 0.7524 1.0831 -0.2194
7 1.3305 0.6311 1.4493 -0.2670
8 0.8324 0.7408 0.5969 -0.3396
9 1.6041 0.7691 0.6687 -0.5147
10 1.4352 0.8069 0.3037 -0.2688
11 2.1468 1.0838 0.2220 0.4311
12 1.9017 0.7628 0.0161 -1.4283
13 1.8683 1.0006 0.0126 0.3698
14 2.1028 0.8491 0.0387 -1.8170
15 2.5943 0.9708 0.0131 -0.5288
################
gibbs100.outflat ##############
Fig. 17.4
The final section of the file contains the sample of size 15 from the posterior over the parameters.
17.2.2 Using an Informative Prior Distribution
Since the model we estimated had four free parameters and only three data points, it is underidentified in the classical setting. In the run from session 17-1 we used a flat, or uninformative prior over the free parameters, and as a result the sampled parameter values vary alot. If you have some information about the values of the parameters, then this can be entered in the form of a prior distribution over the parameters. To enter a prior distribution, you follow exactly the same steps until you are asked the question about flat or informative priors, which you should answer with “i”:
Flat or informative prior (f\i)? [f] i
The prior is a multivariate normal, and is specifed by giving means for each parameter and a variance/covariance matrix over all the parameters. The means for the prior are just the starting values specified (see above). For path coefficients, the prior mean is set to the number that follows the edge in a /graph section, e.g., the /graph section in gibbs100.mod (shown in Fig. 17.3 above). For error variances, the prior mean is set to the number in the /linearmodel section (see Fig. 17.3 also).
The variance/covariance matrix for the prior is set interactively, and cannot be read in from a file currently. The default variance of each free parameter is 16.0, the variance of each fixed parameter is 0.0, and the covariance of any two parameters defaults to 0. Thus the default variance/covariance matrix for the free parameters in the example Lead and iq model is shown in Table 17.1:
|
Var(ele) |
Var(eIQ) |
Var(LE) |
l1 |
l2 |
|||
|
16.0 |
|
|
|
|
|||
|
0.0 |
16.0 |
|
|
|
|||
|
0.0 |
0.0 |
16.0 |
|
|
|||
|
0.0 |
0.0 |
0.0 |
0.0 |
|
|||
|
0.0 |
0.0 |
0.0 |
0.0 |
16.0 |
|||
Table 17.1
Session 17-2 shows how to specify an informative prior distribution for the LEAD-iq example with the multivariate normal distribution over the free parameters we show here (Table. 17.2):
|
|
Var(ele) |
Var(eIQ) |
Var(LE) |
l2 |
|
Mean (m) |
1.0 |
1.0 |
1.0 |
-0.5 |
|
|
Var(ele) |
Var(eIQ) |
Var(LE) |
l2 |
|
|
0.04 |
|
|
|
|
Var/Cov (S) |
0.03 |
0.09 |
|
|
|
|
0.0 |
0.0 |
16.0 |
|
|
|
0.0 |
0.0 |
0.0 |
16.0 |
Table 17.2
Session Gibbs-2
*************************************
Flat or informative prior (f\i)? [f] i
Number of iterations: [10]: 15
Rejection Filename:
[gibbs.rej] <CR>
Default variance for the
Prior: [16]: <CR>
.
After the fixed/free and inequality interaction, TETRAD prints out the default mean and variances for the prior it will use.
Prior
Param. Mean Var
1: eV(le) 1.0000 16.000
2: eV(iq) 1.0000
16.000
3: eV(LE) 1.0000
16.000
4: LE->le 1.0000
0.0000
5: LE->iq -0.5000
16.000
List the numbers of the parameters whose mean, variance, or
covariance you wish to change from its default value in the prior.
Separate them by at least one space, and use no delimiters.
List = 1 2
Picking these two parameters causes TETRAD to prompt, with defaults, for the means, variances, and covariances for each parameter and pair of parameters selected.
Prior mean for eV(le) [ 1.0000
]: <CR>
Variance for eV(le) [
16.0000]: .04
Prior mean for eV(iq) [ 1.0000
]: <CR>
Variance for eV(iq) [ 16.0000]: .09
Since prior knowledge about covariation is more naturally input as correlation, TETRAD prompts for it in this way.
Enter as correlations, not covariances.
Rho[eV(le),eV(iq)] = [ 0.0000
]: .5
Print all free parameters in output file (y\n)? [y] y
*************************************
Because we have imposed a prior distribution over the parameters which is informative about two of the model’s parameters, the output of this run should be quite different than the one before it. Compare the 15 iterations in Fig. 17.5 below with those in Fig. 17.4 above.
################
gibbs100.outprior
##############
Iter eV(le)
eV(iq) eV(LE) LE->iq
1 1.3068 0.9462 0.5033 -0.2762
2 0.9995 0.8233 0.8873 -0.3834
3 1.2424 0.7669 0.9870 -0.4537
4 0.9275 0.8005 1.3329 -0.2638
5 0.8214 1.0296 0.9866 -0.2085
6 1.1325 0.7700 0.9611 -0.2379
7 0.8189 1.0229 1.1040 -0.1543
8 0.7759 0.8990 1.2234 -0.1694
9 0.7574 0.9243 1.0195 -0.1163
10 0.9900 0.7886 1.0554 -0.1729
11 1.1015 0.9043 0.6387 -0.4421
12 0.8376 0.9503 1.2097 -0.2290
13 1.0179 0.7101 0.5682 0.0180
14 1.2011 0.8305 1.2246 -0.3234
15 1.0436 0.8567 0.9570 -0.3466
################
gibbs100.outprior
##############
Fig. 17.5
17.3 The Output of
the Gibbs Module
Each iteration produced by the Gibbs module is a row in the output file, indexed by the iteration number (see Fig. 17.5, for example). The iterations produced by the sampler after it has converged are a sample from the posterior, but not an i.i.d. sample. The iterations are from a dependent sequence that is auto-correlated. In our experience this autocorrelation is completely harmless and has no effect on the properties of the posterior approximated by the sample. If you want to eliminate autocorrelation in the sample, you can keep every kth iteration, e.g., every 25th.
To decide if the sequence has converged, you can split the iterations into 4 contiguous blocks, and calculate distributional characteristics for each block, e.g., qMedian, q.025, and q.975. If the sequence has converged, these quantities should be the same in each of the blocks. If they are similar, but show a steady trend, then the sequence has probably not converged.